Diện tích lăng trụ – Công thức và phương pháp tính toán chi tiết

Diện tích lăng trụ là một trong những kiến thức cốt lõi trong chương trình hình học không gian. Gia Sư VietEdu sẽ cùng các em khám phá chi tiết các công thức tính toán, phương pháp giải bài tập hiệu quả và những ứng dụng thực tiễn. Bài viết tập trung hướng dẫn cách tính diện tích xung quanh, diện tích toàn phần của lăng trụ đứng và lăng trụ xiên, đồng thời cung cấp những bài tập mẫu để các em rèn luyện kỹ năng giải toán.

Diện tích lăng trụ và những thành phần cấu tạo cơ bản

Trước khi đi vào các công thức tính toán, các em cần hiểu rõ cấu trúc của lăng trụ. Lăng trụ là một khối đa diện đặc biệt được tạo thành từ hai mặt đáy có hình dạng giống hệt nhau và được đặt song song với nhau. Nối liền hai mặt đáy này là các mặt bên có dạng hình chữ nhật hoặc hình bình hành tùy thuộc vào loại lăng trụ.

Khi tính diện tích lăng trụ, chúng ta cần quan tâm đến hai thành phần chính: diện tích xung quanh và diện tích hai mặt đáy. Diện tích toàn phần của lăng trụ chính là tổng của hai thành phần này. Công thức tính diện tích xung quanh được xây dựng dựa trên nguyên lý khai triển các mặt bên thành một hình chữ nhật, với chiều dài bằng chu vi đáy và chiều rộng bằng chiều cao lăng trụ.

Đối với lăng trụ đứng, các cạnh bên luôn vuông góc với mặt đáy, khiến việc tính toán trở nên đơn giản hơn rất nhiều. Diện tích xung quanh được tính bằng chu vi đáy nhân với chiều cao. Ví dụ minh họa: một lăng trụ đứng có đáy là hình chữ nhật với các kích thước 3cm × 4cm và chiều cao 5cm sẽ có diện tích xung quanh là (3 + 4) × 2 × 5 = 70 cm².

Mỗi thành phần cấu tạo của lăng trụ – từ mặt đáy, mặt bên, cạnh bên đến các đỉnh – đều có vai trò quan trọng trong việc xác định diện tích tổng thể. Việc hiểu rõ đặc điểm và chức năng của từng thành phần sẽ giúp các em áp dụng công thức một cách chính xác và hiệu quả trong quá trình giải bài tập.

Hệ thống công thức tính diện tích xung quanh và toàn phần lăng trụ đứng

Trong hình học không gian, việc nắm vững các công thức tính diện tích lăng trụ là điều kiện tiên quyết để giải quyết thành công các bài toán từ cơ bản đến nâng cao. VietEdu sẽ hướng dẫn các em hai công thức cơ bản nhất: công thức tính diện tích xung quanh và công thức tính diện tích toàn phần của lăng trụ đứng.

Công thức tính diện tích xung quanh lăng trụ đứng

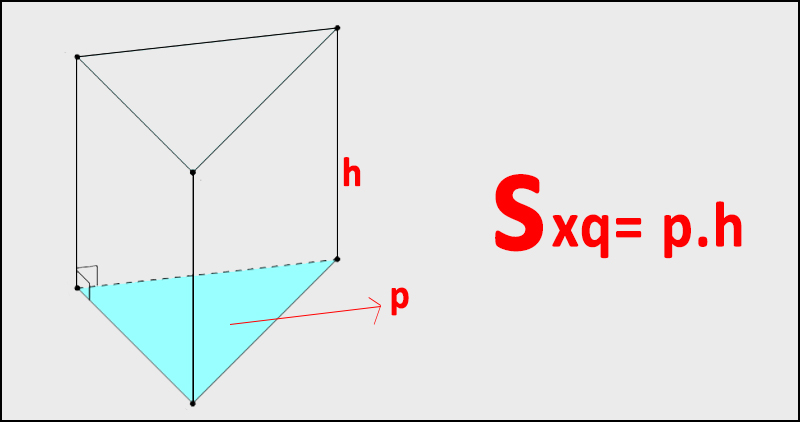
Diện tích xung quanh của lăng trụ đứng được tính bằng tích của chu vi đáy và chiều cao của lăng trụ. Cơ sở lý thuyết của công thức này xuất phát từ việc khi ta khai triển toàn bộ các mặt bên của lăng trụ ra một mặt phẳng, kết quả thu được sẽ là một hình chữ nhật hoàn chỉnh. Hình chữ nhật này có chiều dài bằng chu vi của mặt đáy và chiều rộng chính là chiều cao của lăng trụ.

Sử dụng ký hiệu toán học, nếu gọi Sxq là diện tích xung quanh, P là chu vi đáy và h là chiều cao lăng trụ, ta có công thức:

Sxq = P × h

Công thức này áp dụng cho mọi loại lăng trụ đứng, bất kể mặt đáy có hình dạng như thế nào – tam giác, tứ giác, ngũ giác hay bất kỳ đa giác nào khác.

Công thức tính diện tích toàn phần lăng trụ đứng

Diện tích toàn phần bao gồm cả diện tích xung quanh và diện tích của hai mặt đáy. Đây là thông số quan trọng nhất khi chúng ta cần tính toán lượng vật liệu cần thiết để chế tạo hoặc sơn phủ toàn bộ bề mặt của một vật thể có dạng lăng trụ.

Với Stp là diện tích toàn phần và Sd là diện tích của một mặt đáy, công thức tổng quát được viết như sau:

Stp = Sxq + 2Sd = P × h + 2Sd

Lưu ý quan trọng: diện tích đáy được nhân với 2 vì lăng trụ có hai mặt đáy giống hệt nhau.

Quy trình tính toán diện tích lăng trụ

Để đảm bảo tính chính xác trong quá trình tính toán, VietEdu khuyến nghị các em thực hiện theo quy trình có hệ thống gồm 4 bước cơ bản:

• Bước 1: Phân tích mặt đáy để xác định chu vi và diện tích đáy. Tùy thuộc vào hình dạng đáy (tam giác, hình chữ nhật, hình thang…), áp dụng công thức tương ứng
• Bước 2: Xác định chiều cao của lăng trụ từ dữ kiện đề bài hoặc thông qua đo đạc
• Bước 3: Tính diện tích xung quanh bằng công thức Sxq = P × h
• Bước 4: Tính diện tích toàn phần bằng cách cộng thêm diện tích hai mặt đáy

Việc tuân thủ đúng quy trình này không chỉ giúp tránh sai sót mà còn tạo thói quen làm bài khoa học, có hệ thống cho các em.

Phương pháp giải quyết các dạng bài toán về diện tích lăng trụ

Để thành công trong việc giải các bài toán về diện tích lăng trụ, các em cần kết hợp việc nắm vững công thức với kỹ năng phân tích đề bài và tư duy hình học. VietEdu sẽ hướng dẫn các em phân loại các dạng bài tập thường gặp và phương pháp tiếp cận phù hợp cho từng dạng.

Phân loại các dạng bài tập thường gặp

Dạng bài tập cơ bản: Tính diện tích xung quanh khi đã biết đầy đủ các kích thước của mặt đáy và chiều cao lăng trụ. Đây là dạng bài đơn giản nhất, yêu cầu các em xác định chu vi đáy và áp dụng trực tiếp công thức Sxq = P × h.

Dạng bài tập trung bình: Tính diện tích toàn phần khi biết một phần thông tin như diện tích xung quanh hoặc diện tích đáy. Dạng này đòi hỏi các em phải phân tích mối quan hệ giữa các thành phần diện tích và sử dụng phép biến đổi đại số.

Dạng bài tập nâng cao: Bài toán tổng hợp kết hợp diện tích lăng trụ với các kiến thức khác như thể tích, tỷ lệ các cạnh, hoặc các bài toán tối ưu hóa. Những bài tập này thường xuất hiện trong các kỳ thi quan trọng.

Chiến lược giải bài và những lưu ý quan trọng

Giai đoạn chuẩn bị: Đọc kỹ đề bài, vẽ hình minh họa và ghi chép đầy đủ các dữ kiện đã cho. Việc vẽ hình không chỉ giúp hình dung rõ bài toán mà còn hỗ trợ quá trình phân tích và tìm lời giải.

Giai đoạn phân tích: Xác định rõ những gì đề bài yêu cầu tìm và lựa chọn công thức phù hợp. Đối với các bài toán phức tạp, cần chia nhỏ thành các bước để giải quyết từng phần một cách có hệ thống.

Giai đoạn thực hiện: Tính toán cẩn thận theo từng bước, không bỏ qua các phép tính trung gian. Sau khi có kết quả, kiểm tra lại bằng cách thế ngược vào điều kiện ban đầu hoặc sử dụng phương pháp khác để xác minh.

Bài tập mẫu với lời giải chi tiết

Đề bài: Cho lăng trụ đứng có đáy là tam giác vuông cân với cạnh góc vuông có độ dài 6cm. Chiều cao của lăng trụ là 8cm. Tính diện tích toàn phần của lăng trụ.

Lời giải chi tiết:

Bước 1: Phân tích tam giác đáy vuông cân

• Hai cạnh góc vuông đều bằng 6cm
• Cạnh huyền = 6√2 cm (theo định lý Pythagoras)
• Chu vi đáy = 6 + 6 + 6√2 = (12 + 6√2) cm
• Diện tích đáy = (6 × 6)/2 = 18 cm²

Bước 2: Tính diện tích xung quanh

Sxq = chu vi đáy × chiều cao = (12 + 6√2) × 8 = (96 + 48√2) cm²

Bước 3: Tính diện tích toàn phần

Stp = Sxq + 2 × diện tích đáy = (96 + 48√2) + 2 × 18 = (132 + 48√2) cm²

Vậy diện tích toàn phần của lăng trụ là (132 + 48√2) cm².

Trường hợp đặc biệt: Tính diện tích lăng trụ nghiêng (lăng trụ xiên)

Lăng trụ xiên (hay lăng trụ nghiêng) có đặc điểm khác biệt so với lăng trụ đứng ở chỗ các cạnh bên không vuông góc với mặt đáy. Điều này tạo ra những thách thức mới trong quá trình tính toán diện tích, đòi hỏi các em phải hiểu rõ sự khác biệt về cấu trúc hình học.

Sự khác biệt cơ bản giữa lăng trụ đứng và lăng trụ nghiêng

Với lăng trụ đứng, tất cả các cạnh bên đều tạo với mặt đáy những góc vuông 90°, do đó các mặt bên đều có dạng hình chữ nhật. Ngược lại, trong lăng trụ xiên, các cạnh bên tạo với mặt đáy những góc khác 90°, khiến cho các mặt bên trở thành hình bình hành.

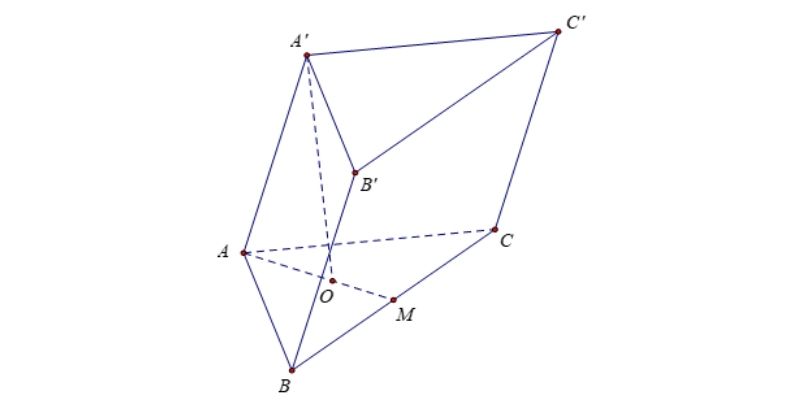
Sự khác biệt này ảnh hưởng trực tiếp đến cách tính diện tích. Trong khi diện tích hình chữ nhật được tính bằng chiều dài nhân chiều rộng, diện tích hình bình hành lại được tính bằng độ dài đáy nhân với chiều cao (là khoảng cách vuông góc giữa hai cạnh đáy song song).

Phương pháp tính diện tích lăng trụ nghiêng

Diện tích toàn phần của lăng trụ xiên vẫn bao gồm diện tích hai mặt đáy cộng với diện tích tất cả các mặt bên. Tuy nhiên, việc tính diện tích các mặt bên phức tạp hơn vì cần xác định chiều cao của hình bình hành, không phải chiều cao của lăng trụ.

Để tính chính xác, các em cần xác định chiều cao vuông góc của mỗi hình bình hành từ một cạnh đáy đến cạnh đáy song song với nó. Diện tích mỗi mặt bên sẽ bằng độ dài cạnh đáy nhân với chiều cao vuông góc này.

Ứng dụng thực tiễn của việc tính diện tích lăng trụ

Kiến thức về diện tích lăng trụ không chỉ quan trọng trong học tập mà còn có nhiều ứng dụng thiết thực trong cuộc sống. Từ ngành kiến trúc xây dựng đến sản xuất công nghiệp, việc tính toán chính xác diện tích lăng trụ giúp tối ưu hóa chi phí và nâng cao hiệu quả sử dụng vật liệu.

Ứng dụng trong ngành kiến trúc và xây dựng

Trong ngành xây dựng hiện đại, hình dạng lăng trụ được sử dụng rộng rãi trong thiết kế các tòa nhà cao tầng, nhà kho, và các công trình công cộng. Theo thống kê từ Hiệp hội Kiến trúc sư Việt Nam, hơn 60% các công trình xây dựng hiện đại áp dụng cấu trúc lăng trụ làm khung chính.

Việc tính toán chính xác diện tích các bề mặt lăng trụ giúp các kỹ sư xác định lượng vật liệu cần thiết như kính cường lực, gạch ốp lát, sơn phủ. Điều này không chỉ giúp kiểm soát chi phí xây dựng mà còn đảm bảo tính thẩm mỹ và chất lượng của công trình.

Một ví dụ tiêu biểu là tòa nhà Bitexco Financial Tower tại TP.HCM, được thiết kế với cấu trúc lăng trụ đa giác phức tạp. Việc tính toán diện tích chính xác đã giúp tối ưu hóa việc sử dụng vật liệu và tạo nên một biểu tượng kiến trúc độc đáo.

Ứng dụng trong thiết kế sản phẩm và sản xuất công nghiệp

Ngành sản xuất công nghiệp hiện đại đã ứng dụng thông minh các tính chất hình học của lăng trụ trong thiết kế bao bì, container và các sản phẩm tiêu dùng. Theo nghiên cứu của Viện Khoa học Công nghệ Việt Nam, việc sử dụng hình dạng lăng trụ trong đóng gói sản phẩm giúp tiết kiệm từ 25-30% không gian lưu trữ so với các hình dạng truyền thống.

Các nhà máy sản xuất thực phẩm và đồ uống đặc biệt ưa chuộng hình dạng lăng trụ cho các sản phẩm đóng hộp vì tính ổn định và khả năng tối ưu hóa không gian vận chuyển. Việc tính toán diện tích chính xác giúp xác định lượng vật liệu bao bì cần thiết và tối ưu hóa chi phí sản xuất.

Các ví dụ cụ thể về lăng trụ trong cuộc sống hàng ngày

Lăng trụ xuất hiện khắp nơi trong cuộc sống hàng ngày của chúng ta. Từ những chiếc hộp bút chì hình lục giác đến các thùng carton đóng gói hàng hóa, tất cả đều áp dụng nguyên lý hình học của lăng trụ. Các công ty vận chuyển quốc tế như DHL, FedEx thiết kế container dựa trên tính toán diện tích lăng trụ để tối ưu hóa không gian chứa hàng.

Trong kiến trúc dân dụng, các cột nhà, dầm kết cấu thường được thiết kế dạng lăng trụ để tăng cường độ chịu lực. Theo số liệu từ Bộ Xây dựng, khoảng 80% các công trình nhà ở hiện đại sử dụng cột lăng trụ làm kết cấu chịu lực chính.

Các công trình công cộng như trường học, bệnh viện, trung tâm thương mại cũng thường được thiết kế theo dạng lăng trụ để tận dụng tối đa diện tích sử dụng và tạo ra không gian thoáng đãng, thuận tiện cho hoạt động của người sử dụng.

Kết luận

Qua bài viết này, Gia Sư VietEdu hy vọng đã giúp các em nắm vững kiến thức về diện tích lăng trụ – một chủ đề quan trọng trong chương trình hình học không gian. Việc thành thạo các công thức tính toán và phương pháp giải bài tập không chỉ giúp các em đạt kết quả tốt trong học tập mà còn cung cấp nền tảng vững chắc cho những ứng dụng thực tiễn trong tương lai. Hãy thường xuyên luyện tập với các dạng bài tập khác nhau để củng cố và nâng cao kỹ năng giải toán của mình.