Diện tích khối cầu – Hướng dẫn công thức và phương pháp tính (kèm ví dụ)

Diện tích khối cầu là một khái niệm cốt lõi trong hình học không gian mà các em cần nắm chắc. Việc thành thạo công thức và ứng dụng của diện tích khối cầu không chỉ hỗ trợ giải bài tập hiệu quả mà còn củng cố nền tảng kiến thức toán học. Gia Sư VietEdu sẽ cùng các em khám phá chi tiết các công thức, phương pháp tính toán và những ứng dụng thực tiễn đa dạng của khái niệm quan trọng này.

Diện tích khối cầu và những khái niệm nền tảng trong hình học không gian

Trong môn Hình học không gian, khối cầu được định nghĩa là tập hợp gồm tất cả các điểm trong không gian ba chiều có cùng khoảng cách đến một điểm cố định được gọi là tâm. Khoảng cách bất biến này chính là bán kính của khối cầu. Khái niệm này giúp các em hình dung một cách rõ ràng về đặc điểm hình dạng và tính chất của khối cầu trong không gian ba chiều.

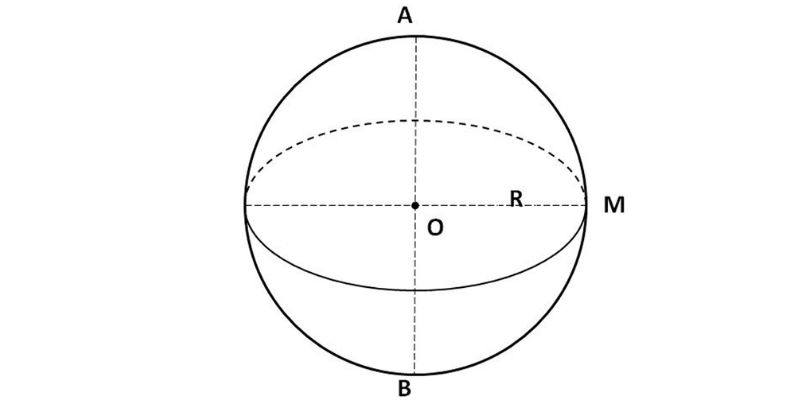
Khi nghiên cứu về diện tích khối cầu, các em cần nắm vững công thức cơ bản S = 4πR², trong đó R đại diện cho bán kính của khối cầu. Công thức quan trọng này được nhà toán học thiên tài Archimedes chứng minh từ thế kỷ thứ 3 trước Công nguyên. Ông đã sử dụng phương pháp toán học vô cùng tinh vi để chứng minh rằng diện tích mặt cầu bằng chính xác diện tích của hình trụ ngoại tiếp khối cầu trừ đi diện tích của hai mặt đáy.

Việc tính toán diện tích khối cầu mang ý nghĩa quan trọng trong nhiều lĩnh vực thực tiễn như kiến trúc, kỹ thuật và thiên văn học hiện đại. Ví dụ điển hình, các kỹ sư hàng không vũ trụ cần tính toán chính xác diện tích bề mặt của các vệ tinh nhân tạo để thiết kế lớp vỏ bảo vệ và bố trí tấm pin năng lượng mặt trời một cách tối ưu. Theo dữ liệu từ NASA, vệ tinh viễn thông Intelsat VI với đường kính 3.6m có diện tích bề mặt xấp xỉ 40.7m².

Hệ thống công thức tính diện tích khối cầu và các thành phần liên quan

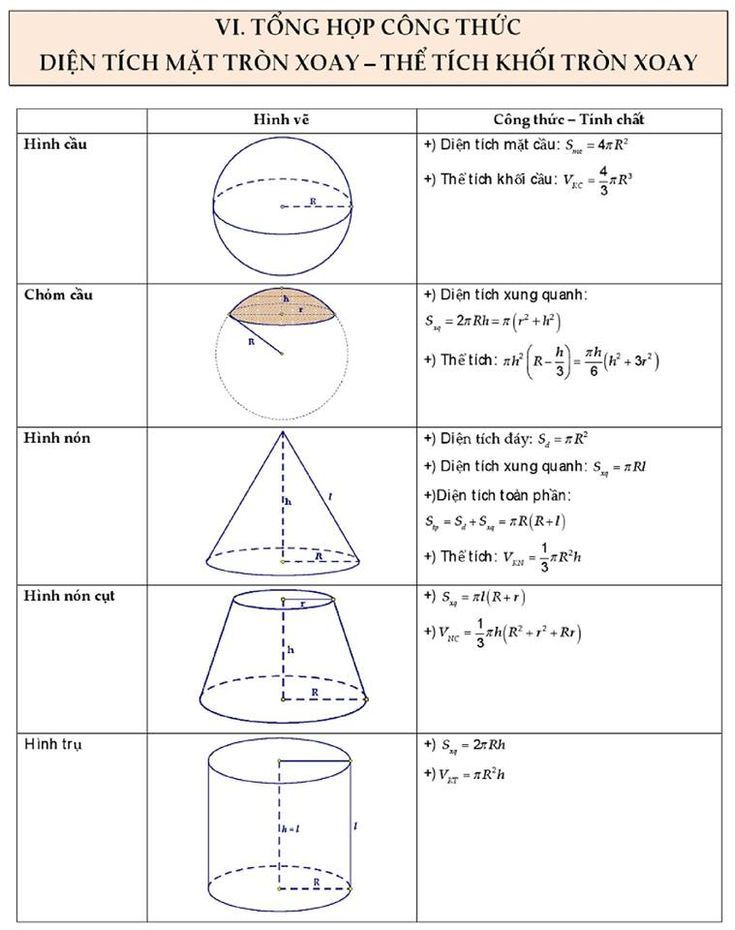
Để tính toán diện tích khối cầu một cách chính xác và toàn diện, Gia Sư VietEdu hướng dẫn các em cần nắm rõ các công thức tính diện tích mặt cầu, diện tích xung quanh và diện tích toàn phần. Mỗi thành phần đều có công thức riêng biệt và đặc điểm tính toán khác nhau. Việc hiểu rõ định nghĩa về hình mặt cầu là nền tảng quan trọng để các em có thể tính toán chính xác các loại diện tích này.

Công thức tính diện tích mặt cầu cơ bản

Diện tích mặt cầu được tính theo công thức chuẩn S = 4πR², trong đó R là bán kính của hình cầu. Công thức này có tính chất tổng quát, áp dụng được cho mọi mặt cầu bất kể vị trí hay hướng của mặt cầu trong không gian ba chiều. Khi áp dụng công thức này, các em cần đặc biệt chú ý đến việc thống nhất đơn vị của bán kính để đảm bảo kết quả chính xác.

Một ví dụ thực tế ấn tượng từ NASA cho thấy diện tích bề mặt Trái Đất xấp xỉ 510 triệu km² được tính dựa trên công thức này với bán kính Trái Đất trung bình là 6.371 km. Kết quả tính toán này đóng vai trò quan trọng giúp các nhà khoa học nghiên cứu về biến đổi khí hậu và địa lý toàn cầu.

Công thức tính diện tích xung quanh khối cầu

Công thức diện tích xung quanh khối cầu được tính bằng công thức Sxq = 4πR². Điều đặc biệt và thú vị là diện tích xung quanh khối cầu hoàn toàn bằng với diện tích mặt cầu do tính đối xứng hoàn hảo đặc trưng của hình cầu.

Trong thực tiễn, công thức này thường được ứng dụng rộng rãi trong thiết kế các vật thể hình cầu như bóng thể thao hay các thiết bị chiếu sáng hiện đại. Các nhà sản xuất thường sử dụng công thức này để tính toán chính xác lượng vật liệu cần thiết cho việc bọc hoặc phủ bề mặt sản phẩm.

Công thức tính diện tích toàn phần khối cầu

Diện tích toàn phần khối cầu cũng chính là diện tích xung quanh khối cầu do hình cầu không có các mặt đáy hay đỉnh như các khối đa diện khác. Công thức tính Stp = 4πR² áp dụng cho mọi trường hợp. Điều này tạo ra sự khác biệt rõ rệt so với các khối đa diện khác thường có diện tích toàn phần bằng tổng của diện tích xung quanh và diện tích các mặt đáy.

Trong ngành công nghiệp sản xuất hiện đại, công thức này được sử dụng một cách rộng rãi để tính toán chi phí sơn phủ hoặc mạ kim loại cho các sản phẩm có hình dạng cầu. Ví dụ, các nhà sản xuất pin năng lượng mặt trời dạng cầu áp dụng công thức này để tối ưu hóa diện tích tiếp xúc với ánh sáng mặt trời.

Phương pháp giải quyết bài tập về diện tích khối cầu

Phương pháp giải bài tập về diện tích khối cầu cần được xây dựng dựa trên các công thức cơ bản và nguyên tắc hình học không gian. Diện tích mặt cầu luôn được tính theo công thức S = 4πR², trong đó R là bán kính của hình cầu. Gia Sư VietEdu khuyến khích các em cần có sự hiểu biết sâu sắc về mối quan hệ giữa các yếu tố như bán kính, đường kính và diện tích, đặc biệt trong các trường hợp khối cầu tiếp xúc với các hình khối khác.

Phân loại các dạng bài tập thường gặp

Trong chương trình hình học không gian, các bài tập tính diện tích khối cầu thường xuất hiện dưới nhiều dạng đa dạng. Dạng phổ biến nhất là bài tập tính diện tích mặt cầu khi đã biết trước bán kính hoặc đường kính của khối cầu.

Ngoài ra còn có các bài toán có độ phức tạp cao hơn như tính diện tích mặt cầu nội tiếp, ngoại tiếp các khối đa diện. Mỗi dạng bài tập đều có những đặc thù riêng biệt và đòi hỏi cách tiếp cận khác nhau để giải quyết hiệu quả.

Phương pháp giải và quy trình thực hiện

Để giải thành công các bài toán về diện tích khối cầu ngoại tiếp, các em cần tuân thủ một quy trình giải có hệ thống và khoa học. Bước đầu tiên là xác định rõ ràng các yếu tố đã cho trong đề bài và phân tích mối quan hệ giữa chúng.

Tiếp theo là vẽ hình minh họa chính xác và đầy đủ, thể hiện tất cả các yếu tố liên quan trong bài toán. Việc này giúp các em hình dung rõ ràng hơn về bài toán và tìm ra hướng giải quyết phù hợp nhất.

Cuối cùng là áp dụng các công thức, định lý đã học để tìm ra kết quả chính xác. Các em cần kiểm tra lại kết quả bằng cách thế ngược vào các điều kiện ban đầu của bài toán.

Bài tập về diện tích mặt cầu đơn giản

Với các bài tập cơ bản, việc tính diện tích mặt cầu thường chỉ cần áp dụng trực tiếp công thức S = 4πR². Tuy nhiên, các em cần đặc biệt chú ý đến đơn vị đo và thực hiện quy đổi phù hợp khi cần thiết.

Ví dụ thực tế từ sách giáo khoa Toán 12: Cho hình cầu có bán kính R = 5cm. Tính diện tích mặt cầu. Áp dụng công thức: S = 4 × 3,14 × 5² = 314 (cm²).

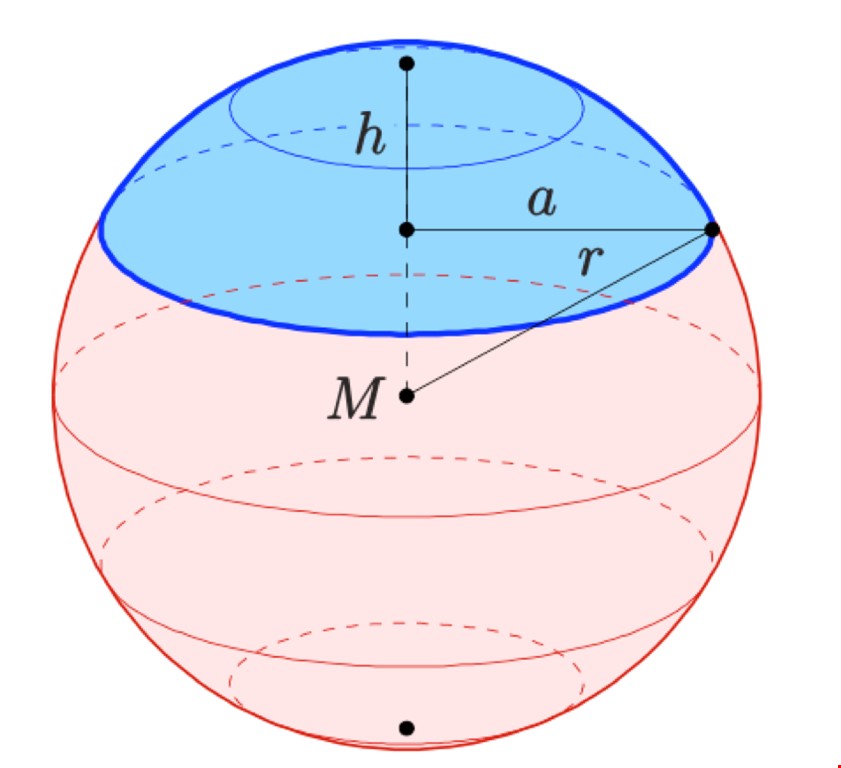
Bài tập về diện tích khối cầu ngoại tiếp

Đối với bài tập về khối cầu ngoại tiếp, các em cần xác định mối quan hệ giữa bán kính khối cầu và kích thước của hình ngoại tiếp. Thông thường, bán kính khối cầu sẽ bằng một nửa đường chéo của hình được ngoại tiếp.

Việc giải loại bài tập này đòi hỏi kiến thức tổng hợp về hình học phẳng và hình học không gian. Đặc biệt quan trọng là các định lý về đường vuông góc và khoảng cách trong không gian.

Mối quan hệ giữa khối cầu với các hình khối khác trong không gian

Khối cầu có mối quan hệ đặc biệt với các hình khối khác trong không gian thông qua các dạng tiếp xúc nội tiếp và ngoại tiếp. Diện tích mặt cầu sẽ có sự biến đổi tùy thuộc vào kích thước của hình khối mà nó tiếp xúc.

Khi khối cầu ngoại tiếp một hình khối, bán kính mặt cầu sẽ lớn hơn kích thước lớn nhất của hình khối đó. Ngược lại, với khối cầu nội tiếp, bán kính mặt cầu nhỏ hơn kích thước nhỏ nhất của hình khối. Điều này tạo nên mối liên hệ chặt chẽ giữa diện tích của các hình khối và diện tích mặt cầu trong các trường hợp tiếp xúc.

Khối cầu nội tiếp và ngoại tiếp

Khối cầu nội tiếp là khối cầu nằm hoàn toàn bên trong một hình khối và tiếp xúc với tất cả các mặt của hình khối đó. Tâm của khối cầu nội tiếp chính là giao điểm của các đường phân giác của các góc đa diện.

Khối cầu ngoại tiếp là khối cầu chứa hoàn toàn một hình khối bên trong nó, với tất cả các đỉnh của hình khối đều nằm trên mặt cầu. Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật phụ thuộc trực tiếp vào đường chéo của khối hộp, chính là đường kính của mặt cầu ngoại tiếp.

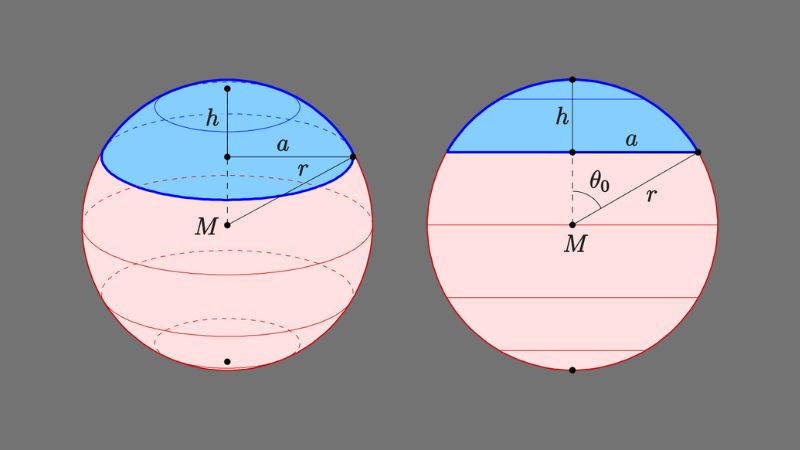
Diện tích mặt cầu trong các trường hợp đặc biệt

Khi khối cầu tiếp xúc với các hình khối đặc biệt như khối lập phương hay hình trụ tròn xoay, diện tích mặt cầu có những mối quan hệ đặc trưng. Với khối lập phương, diện tích mặt cầu nội tiếp bằng 1/4 diện tích mặt cầu ngoại tiếp.

Trong trường hợp khối cầu tiếp xúc với hình trụ tròn xoay, diện tích mặt cầu có mối liên hệ trực tiếp với chiều cao và bán kính đáy của hình trụ. Nếu khối cầu nội tiếp hình trụ, diện tích mặt cầu sẽ nhỏ hơn tổng diện tích xung quanh và hai đáy của hình trụ.

Ứng dụng thực tiễn của diện tích khối cầu trong đời sống

Diện tích khối cầu có nhiều ứng dụng quan trọng trong thực tế, từ lĩnh vực xây dựng đến công nghiệp và đời sống hàng ngày. Việc tính toán chính xác diện tích bề mặt của các cấu trúc hình cầu giúp tối ưu hóa chi phí vật liệu và đảm bảo tính thẩm mỹ cho công trình. Gia Sư VietEdu nhận thấy các ứng dụng khối cầu trong thực tế đã và đang mang lại nhiều giá trị thiết thực cho xã hội.

Ứng dụng trong kiến trúc và xây dựng hiện đại

Trong kiến trúc hiện đại, các mái vòm hình cầu thường được sử dụng để tạo ra không gian rộng lớn mà không cần sử dụng cột chống. Nhà hát Sydney Opera House là ví dụ điển hình với hệ thống mái vòm hình cầu độc đáo, được thiết kế bởi kiến trúc sư tài năng Jørn Utzon. Việc tính toán chính xác diện tích bề mặt giúp xác định lượng vật liệu cần thiết và ước tính chi phí xây dựng.

Các công trình thể thao như sân vận động cũng thường áp dụng kiến trúc mái vòm hình cầu. Allianz Arena ở Munich, Đức sử dụng cấu trúc này không chỉ để che chắn mưa nắng mà còn tạo ra hiệu ứng ánh sáng ấn tượng nhờ hệ thống đèn LED được lắp đặt trên toàn bộ bề mặt.

Ứng dụng trong khoa học kỹ thuật

Ngành công nghiệp sản xuất bình áp lực và bồn chứa thường sử dụng hình dạng cầu để tối ưu hóa khả năng chịu áp suất. Các bồn chứa khí đốt LPG hình cầu có khả năng phân bố áp suất đồng đều trên toàn bộ bề mặt, giảm thiểu nguy cơ nứt vỡ do tập trung ứng suất.

Trong lĩnh vực hàng không vũ trụ, các ăng-ten radar được thiết kế dạng hình cầu để thu phát sóng với hiệu quả tối ưu nhất. Đài thiên văn Arecibo ở Puerto Rico từng sở hữu chảo thu sóng vô tuyến hình cầu lớn nhất thế giới với đường kính 305m.

Ứng dụng trong đời sống hàng ngày

Các thiết bị chiếu sáng như bóng đèn tròn hay đèn trang trí dạng cầu được sử dụng phổ biến trong trang trí nội thất. Nhờ hình dạng cầu, ánh sáng được phân tán đều và tạo ra hiệu ứng thẩm mỹ cao.

Trong thể thao, quả bóng đá, bóng rổ hay bóng tennis đều có hình dạng gần với hình cầu hoàn hảo. Việc tính toán diện tích bề mặt chính xác giúp kiểm soát độ nảy và khí động học của bóng, đảm bảo tính công bằng trong thi đấu.

Các dụng cụ nhà bếp như nồi, chảo cũng thường có đáy hình cầu để tăng hiệu quả truyền nhiệt và phân bố nhiệt đồng đều. Thiết kế này giúp thức ăn chín đều và tiết kiệm năng lượng khi nấu nướng.

Kết luận

Qua bài viết này, Gia Sư VietEdu hy vọng đã giúp các em nắm vững kiến thức về diện tích khối cầu – một khái niệm quan trọng trong toán học, đặc biệt trong hình học không gian. Việc thành thạo các công thức tính diện tích khối cầu cũng như các phương pháp giải bài tập liên quan sẽ giúp các em giải quyết nhiều bài toán và ứng dụng thực tế trong cuộc sống. Hãy thực hành thường xuyên với các dạng bài tập đa dạng để nâng cao trình độ toán học của mình.