Diện tích hình chóp cụt – Công thức và phương pháp tính (kèm ví dụ)

Diện tích hình chóp cụt là một khái niệm trọng tâm trong hình học không gian. Gia Sư VietEdu sẽ cùng các em tìm hiểu chi tiết về công thức, phương pháp tính và những ứng dụng thực tiễn của diện tích hình chóp cụt trong toán học. Bài viết hướng dẫn các em nắm vững cách tính diện tích xung quanh, diện tích đáy cũng như phân tích từng thành phần để hiểu sâu hơn về khối hình học đặc biệt này.

Diện tích hình chóp cụt và những thành phần hình học cơ bản

Để hiểu rõ về diện tích hình chóp cụt, các em cần nắm vững định nghĩa về hình chóp cụt. Đây là một khối đa diện đặc biệt được hình thành khi ta thực hiện phép cắt một hình chóp hoàn chỉnh bởi một mặt phẳng song song với đáy mà không đi qua đỉnh của hình chóp đó. Kết quả là ta sẽ có một khối hình có hai mặt đáy song song với nhau và các mặt bên đều có dạng hình thang.

Khi tính diện tích hình chóp cụt, chúng ta cần tính tổng của ba thành phần chính: diện tích mặt đáy lớn, diện tích mặt đáy nhỏ và diện tích tất cả các mặt bên. Công thức tổng quát có dạng S = S1 + S2 + Sb, trong đó S1 và S2 lần lượt là diện tích của hai mặt đáy còn Sb là tổng diện tích các mặt bên. Việc nắm chắc công thức này là nền tảng để các em giải quyết thành công các bài toán hình học không gian.

Đặc điểm nổi bật của hình chóp cụt thể hiện ở cấu trúc hình học độc đáo. Hai mặt đáy song song có hình dạng tương tự nhau nhưng kích thước khác biệt, với mặt đáy phía trên luôn có kích thước nhỏ hơn mặt đáy phía dưới. Các cạnh bên của hình chóp cụt không song song mà nghiêng về phía trong, và nếu ta kéo dài các cạnh này thì chúng sẽ hội tụ tại một điểm – chính là đỉnh của hình chóp ban đầu trước khi bị cắt.

Trong thực tiễn, hình chóp cụt xuất hiện rất phổ biến trong kiến trúc và xây dựng. Một ví dụ tiêu biểu là cấu trúc thân tháp Eiffel tại Paris được thiết kế dựa trên nguyên lý hình chóp cụt, giúp công trình vừa đạt được tính thẩm mỹ cao vừa đảm bảo độ ổn định và khả năng chịu lực tối ưu.

Hệ thống công thức tính diện tích xung quanh và diện tích đáy hình chóp cụt

Để tính toán chính xác diện tích hình chóp cụt, Gia Sư VietEdu hướng dẫn các em cần xác định được hai thành phần cơ bản: diện tích xung quanh và diện tích của cả hai mặt đáy. Những công thức này không chỉ giúp giải quyết các bài toán lý thuyết mà còn có ứng dụng rộng rãi trong thực tế, từ thiết kế kiến trúc đến tính toán vật liệu xây dựng.

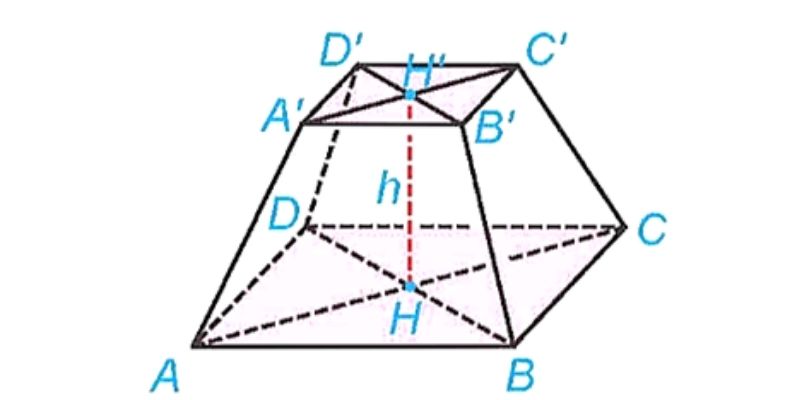
Quá trình tính toán diện tích hình chóp cụt đòi hỏi sự kết hợp khéo léo giữa việc tính diện tích xung quanh và diện tích các mặt đáy. Trong đó, diện tích xung quanh được xác định bằng tổng diện tích của tất cả các mặt bên hình thang, còn diện tích đáy bao gồm diện tích của hai mặt đáy song song có kích thước khác nhau.

Phương pháp tính diện tích xung quanh hình chóp cụt

Diện tích xung quanh hình chóp cụt được tính bằng tổng diện tích của tất cả các mặt bên, mỗi mặt bên đều có dạng hình thang. Để tính diện tích mỗi hình thang, các em cần xác định được chiều cao của hình thang (chính là độ cao mặt bên) và độ dài hai đáy song song (là các cạnh tương ứng của hai đáy hình chóp cụt).

Trong trường hợp đặc biệt khi hình chóp cụt có đáy là hình tròn, diện tích xung quanh sẽ có dạng một mặt cong đặc biệt. Công thức tính trong trường hợp này là Sxq = π(R + r)l, với R là bán kính đáy lớn, r là bán kính đáy nhỏ và l là độ dài đường sinh của hình chóp cụt.

Cách xác định diện tích đáy hình chóp cụt

Diện tích đáy hình chóp cụt là tổng diện tích của hai mặt đáy song song. Tùy thuộc vào hình dạng cụ thể của các mặt đáy, các em sẽ áp dụng các công thức tính diện tích tương ứng. Ví dụ, nếu đáy là hình vuông thì áp dụng công thức diện tích hình vuông, nếu đáy là hình tròn thì sử dụng công thức diện tích hình tròn.

Khi thực hiện tính toán, các em cần đặc biệt chú ý đến tỷ lệ kích thước giữa hai mặt đáy song song. Đối với hình chóp cụt đều, tỷ lệ này sẽ giúp xác định mối liên hệ giữa các kích thước của hai đáy, từ đó có thể tính toán chính xác diện tích của từng mặt đáy.

Phương pháp tính diện tích toàn phần hình chóp cụt

Diện tích toàn phần hình chóp cụt được tính bằng tổng của diện tích hai mặt đáy và diện tích tất cả các mặt bên. Công thức này có tính chất tổng quát, áp dụng được cho mọi dạng hình chóp cụt, từ những hình có đáy tam giác, tứ giác cho đến các đa giác đều phức tạp hơn.

Để có thể tính toán chính xác diện tích hình chóp cụt, các em cần xác định rõ ràng các thông số cơ bản như kích thước của hai mặt đáy và chiều cao của hình chóp cụt. Việc tính diện tích các mặt bên thường đòi hỏi phải vận dụng định lý Pythagoras và các kiến thức về tam giác vuông để tìm ra các yếu tố chưa biết.

Quy trình tính diện tích toàn phần từng bước

Bước 1: Xác định diện tích mặt đáy lớn (S1) và diện tích mặt đáy nhỏ (S2) dựa vào hình dạng cụ thể của các mặt đáy.

Bước 2: Tính độ dài cạnh bên của hình chóp cụt sử dụng công thức l = √(h² + (R-r)²), trong đó h là chiều cao và R, r lần lượt là “bán kính” của đáy lớn và đáy nhỏ.

Bước 3: Tính diện tích các mặt bên bằng công thức Sb = (P1 + P2)l/2, với P1, P2 lần lượt là chu vi của đáy lớn và đáy nhỏ.

Bước 4: Áp dụng công thức tổng hợp diện tích toàn phần: S = S1 + S2 + Sb

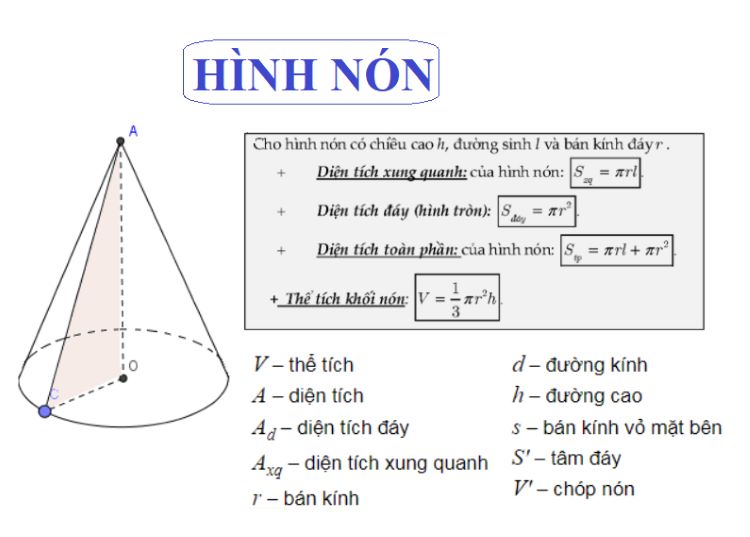
Ví dụ minh họa cụ thể

Đề bài: Cho hình chóp cụt có đáy là hình vuông, cạnh đáy lớn a = 8cm, cạnh đáy nhỏ b = 4cm, chiều cao h = 6cm. Tính diện tích toàn phần.

Lời giải chi tiết:

Diện tích đáy lớn: S1 = a² = 8² = 64cm²

Diện tích đáy nhỏ: S2 = b² = 4² = 16cm²

Độ dài cạnh bên: l = √(6² + (4-2)²) = √(36 + 4) = √40 ≈ 6.32cm

Diện tích mặt bên: Sb = (32 + 16) × 6.32/2 = 48 × 3.16 = 151.68cm²

Vậy diện tích toàn phần = 64 + 16 + 151.68 = 231.68cm²

Hướng dẫn giải các dạng bài toán về diện tích hình chóp cụt

Để giải thành công các bài toán về diện tích hình chóp cụt, các em cần nắm vững phương pháp xác định diện tích xung quanh và diện tích hai mặt đáy. Diện tích toàn phần luôn bằng tổng của diện tích xung quanh và diện tích hai đáy. Quá trình tính toán cần dựa trên các yếu tố quan trọng như chiều cao, độ dài cạnh bên, góc nghiêng và kích thước của cả hai mặt đáy.

Khi giải các bài toán liên quan đến thể tích và diện tích, Gia Sư VietEdu khuyến khích các em thường xuyên kết hợp kiến thức về diện tích hình chóp cụt với các kiến thức khác để giải quyết những bài toán có độ phức tạp cao hơn. Việc thành thạo các công thức và phương pháp tính toán sẽ giúp các em xử lý hiệu quả nhiều dạng bài tập đa dạng.

Chiến lược phân tích và lập phương án giải

Bước đầu tiên khi tiếp cận bài toán về diện tích hình chóp cụt là phân tích cẩn thận dữ kiện mà đề bài cung cấp. Các em cần xác định rõ ràng loại hình chóp cụt đang xét (có đáy tam giác, tứ giác hay đa giác đều), các kích thước đã biết và những yêu cầu cần giải quyết.

Tiếp theo, việc vẽ hình phụ sẽ giúp các em hình dung rõ ràng mối quan hệ giữa các yếu tố trong bài toán. Việc vẽ các đường vuông góc, hình chiếu và thiết diện sẽ hỗ trợ nhận diện các tam giác đồng dạng, từ đó tìm ra các tỷ số và mối liên hệ cần thiết.

Cuối cùng là xây dựng phương án giải theo một trình tự logic rõ ràng: tính toán các yếu tố trung gian cần thiết, áp dụng công thức phù hợp và kiểm tra tính hợp lý của kết quả thu được.

Các dạng bài tập thường gặp và phương pháp giải

Dạng 1: Tính diện tích xung quanh khi đã biết kích thước của hai mặt đáy và chiều cao. Với dạng bài này, các em cần tính độ dài đường sinh và áp dụng công thức diện tích hình thang cho từng mặt bên.

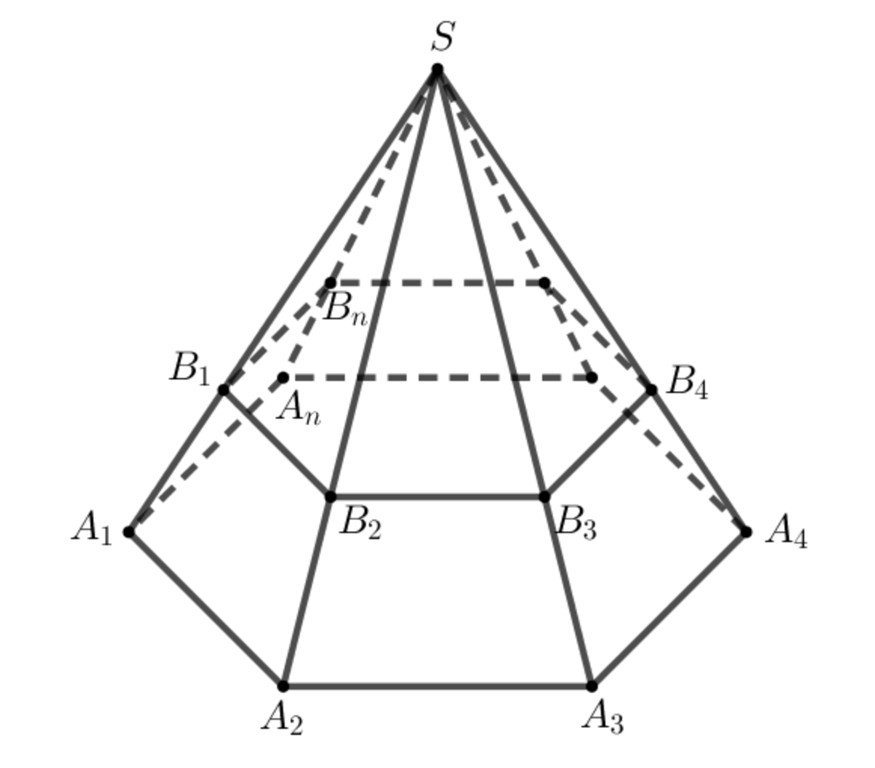
Dạng 2: Tính diện tích toàn phần khi biết góc nghiêng và một số kích thước nhất định. Trong trường hợp này, các em cần vận dụng kiến thức về tam giác vuông và các tỷ số lượng giác để tìm ra các yếu tố chưa biết.

Một ví dụ thực tế thường gặp là bài toán tính diện tích vỏ của một chiếc phễu hình chóp cụt có đường kính đáy lớn 30cm, đường kính đáy nhỏ 10cm và chiều cao 40cm. Việc giải quyết bài toán này đòi hỏi các em phải tính cả diện tích xung quanh và diện tích của hai mặt đáy hình tròn.

Ứng dụng thực tiễn của diện tích hình chóp cụt trong cuộc sống

Diện tích hình chóp cụt là một công cụ toán học có giá trị ứng dụng cao, được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau. Việc tính toán chính xác diện tích của các cấu trúc hình chóp cụt giúp tối ưu hóa quá trình thiết kế và thi công trong thực tiễn. Gia Sư VietEdu nhận thấy rằng ứng dụng của diện tích hình chóp cụt đóng vai trò then chốt trong việc đảm bảo tính chính xác và hiệu quả kinh tế của nhiều công trình quan trọng.

Ứng dụng trong lĩnh vực kiến trúc và xây dựng

Trong ngành kiến trúc hiện đại, các cấu trúc hình chóp cụt thường được sử dụng trong thiết kế mái nhà, tháp chuông và các công trình tôn giáo. Việc tính toán chính xác diện tích bề mặt giúp kiến trúc sư xác định lượng vật liệu cần thiết và ước tính chi phí thi công một cách chính xác nhất.

Các công trình kiến trúc hiện đại như tòa nhà Burj Al Arab tại Dubai đã sử dụng hình dạng chóp cụt để tạo nên vẻ đẹp độc đáo và tối ưu hóa khả năng chống chịu gió bão. Kiến trúc sư đã áp dụng nguyên lý này để thiết kế nên tòa nhà biểu tượng có hình dáng cánh buồm đầy ấn tượng.

Trong xây dựng cầu đường và các công trình giao thông, các trụ cầu thường được thiết kế theo dạng hình chóp cụt để tăng cường độ vững chắc và khả năng chịu lực. Ứng dụng kiến thức về hình chóp cụt trong toán học đã giúp các kỹ sư tính toán chính xác lượng bê tông và thép cần thiết, đảm bảo tính kinh tế và an toàn tối đa cho công trình.

Ứng dụng trong công nghiệp sản xuất

Trong ngành công nghiệp đúc kim loại, các khuôn đúc thường có dạng hình chóp cụt để thuận tiện cho quá trình tháo lắp sản phẩm. Nhiều công ty sản xuất ô tô đã áp dụng nguyên lý này trong thiết kế khuôn đúc các chi tiết, giúp tăng năng suất sản xuất đáng kể.

Các ống khói của nhà máy thường được thiết kế theo dạng hình chóp cụt để tối ưu hóa luồng khí thải và tăng cường độ bền của công trình. Nghiên cứu khoa học đã chỉ ra rằng thiết kế này giúp giảm đáng kể sức cản không khí so với các ống khói hình trụ truyền thống.

Trong sản xuất bao bì, các hộp giấy có dạng hình chóp cụt được ưa chuộng do khả năng xếp chồng tối ưu và tiết kiệm không gian lưu trữ. Thiết kế này không chỉ giúp giảm chi phí vận chuyển và bảo quản mà còn tăng tính thẩm mỹ cho sản phẩm.

Kết luận

Qua bài viết này, Gia Sư VietEdu hy vọng đã giúp các em nắm vững kiến thức về diện tích hình chóp cụt – một khái niệm quan trọng trong hình học không gian với nhiều ứng dụng thực tiễn. Việc thành thạo các công thức tính diện tích xung quanh, diện tích đáy và diện tích toàn phần sẽ giúp các em giải quyết thành công các bài toán liên quan. Hãy thường xuyên luyện tập với các dạng bài tập khác nhau để củng cố và nâng cao kỹ năng toán học của mình.