Công thức Heron – Hướng dẫn phương pháp tính diện tích tam giác khi biết ba cạnh

Công thức Heron là phương pháp hiệu quả để tính diện tích tam giác khi biết độ dài ba cạnh. Thông qua bài viết này, Gia Sư VietEdu sẽ cùng các em khám phá cách phát biểu, ứng dụng cũng như các bước áp dụng công thức Heron trong hình học phẳng. Nội dung sẽ hệ thống hóa kiến thức, từ chứng minh đến bài tập, giúp các em tăng cường kỹ năng toán học một cách toàn diện.

Công thức Heron là phương pháp tính diện tích tam giác khi biết độ dài ba cạnh

Công thức Heron là một phương pháp toán học cổ đại được phát triển bởi nhà toán học Heron thành Alexandria vào khoảng thế kỷ thứ nhất sau Công nguyên. Phương pháp này giúp tính diện tích tam giác khi biết độ dài 3 cạnh mà không cần thông qua các yếu tố khác như góc hay đường cao.

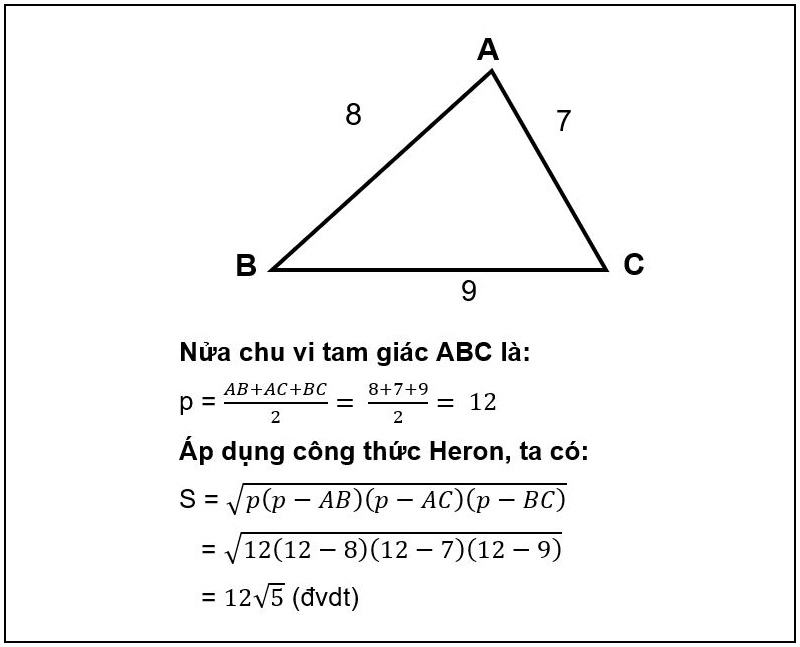
Theo công thức Heron, diện tích tam giác được tính bằng căn bậc hai của tích p(p-a)(p-b)(p-c), trong đó p là nửa chu vi tam giác và a, b, c là độ dài ba cạnh. Cụ thể, p = (a+b+c)/2 và diện tích S = √[p(p-a)(p-b)(p-c)]. Đây là một công thức đơn giản nhưng mạnh mẽ, được ứng dụng rộng rãi trong hình học và các lĩnh vực kỹ thuật.

Công thức Heron đặc biệt hữu ích khi chỉ có thông tin về độ dài các cạnh của tam giác. Ví dụ, trong ngành xây dựng, khi cần tính diện tích một mảnh đất hình tam giác mà chỉ đo được độ dài các cạnh, công thức Heron sẽ cho kết quả chính xác mà không cần đo thêm các yếu tố khác. Tương tự trong thiết kế đồ họa, công thức này giúp tính toán diện tích các hình tam giác một cách nhanh chóng và chính xác.

Gia Sư VietEdu nhận thấy rằng việc nắm vững công thức Heron không chỉ giúp các em giải quyết các bài toán hình học cơ bản mà còn mở ra cánh cửa cho những ứng dụng thực tiễn quan trọng trong cuộc sống.

Cách phát biểu và ứng dụng công thức Heron trong hình học phẳng

Công thức Heron là một phương pháp tính diện tích tam giác khi biết độ dài 3 cạnh, được phát biểu bởi nhà toán học Heron thành Alexandria. Công thức Heron đặc biệt hữu ích trong Hình học phẳng khi không thể áp dụng các công thức thông thường.

Theo đó, diện tích tam giác S được tính bằng căn bậc hai của tích p(p-a)(p-b)(p-c), trong đó p là nửa chu vi tam giác và a, b, c là độ dài ba cạnh. Công thức Heron này giúp tính diện tích tam giác một cách chính xác mà không cần thông qua góc hay đường cao.

Công thức Heron có ưu điểm là áp dụng được cho mọi tam giác, không phụ thuộc vào hình dạng hay góc. Điều này làm cho công thức Heron trở thành công cụ quan trọng trong việc giải các bài toán hình học phức tạp, đặc biệt là những bài toán liên quan đến diện tích tam giác không đều.

Trong thực tế, công thức Heron được ứng dụng rộng rãi trong nhiều lĩnh vực như xây dựng, kiến trúc và đo đạc địa hình. Ví dụ, khi cần tính diện tích một mảnh đất hình tam giác không đều, việc đo 3 cạnh và áp dụng công thức Heron sẽ cho kết quả chính xác và nhanh chóng hơn so với các phương pháp truyền thống.

Các bước áp dụng công thức Heron để tính diện tích tam giác

Việc áp dụng công thức Heron giúp tính chính xác diện tích của mọi tam giác khi biết độ dài 3 cạnh. Phương pháp này đặc biệt hữu ích với các tam giác không đều hoặc khó xác định đường cao.

Để thực hiện tính diện tích tam giác theo công thức Heron, Gia Sư VietEdu hướng dẫn các em cần thực hiện tuần tự 3 bước. Mỗi bước đều quan trọng và cần được tính toán cẩn thận để đảm bảo kết quả chính xác.

Xác định độ dài ba cạnh tam giác

Bước đầu tiên để áp dụng công thức Heron là đo lường chính xác độ dài 3 cạnh của tam giác, thường được ký hiệu là a, b và c. Việc đo đạc cần được thực hiện bằng thước đo phù hợp, có độ chính xác cao.

Với tam giác trên giấy, có thể sử dụng thước kẻ thông thường. Đối với tam giác trong thực tế, nên dùng thước dây hoặc máy đo laser để đảm bảo độ chính xác tối đa khi áp dụng công thức Heron.

Tính nửa chu vi tam giác p=(a+b+c)/2

Sau khi có độ dài 3 cạnh, tiến hành tính nửa chu vi p bằng cách cộng độ dài 3 cạnh rồi chia 2. Công thức Heron này được phát triển từ thế kỷ thứ nhất và đã được chứng minh tính đúng đắn qua nhiều thế kỷ.

Việc tính nửa chu vi p là bước trung gian quan trọng trong công thức Heron, giúp đơn giản hóa công thức cuối cùng. Các em cần kiểm tra kỹ kết quả tính p trước khi chuyển sang bước tiếp theo.

Áp dụng công thức S=√(p(p-a)(p-b)(p-c))

Bước cuối cùng trong việc áp dụng công thức Heron là thay các giá trị đã tính vào công thức S=√(p(p-a)(p-b)(p-c)). Lưu ý thực hiện đúng thứ tự các phép tính trong dấu căn bậc hai.

Trước tiên tính các hiệu (p-a), (p-b), (p-c), sau đó nhân với p và các hiệu với nhau. Cuối cùng tính căn bậc hai của tích thu được để ra kết quả diện tích tam giác theo công thức Heron.

Kết quả tính toán cần được kiểm tra lại bằng cách so sánh với các phương pháp khác hoặc ước lượng sơ bộ để đảm bảo tính chính xác của công thức Heron.

Chứng minh công thức Heron dựa trên các hệ thức lượng giác

Chứng minh công thức Heron là một bài toán quan trọng trong hình học, giúp tính diện tích tam giác khi biết độ dài ba cạnh. Phương pháp này được đặt theo tên của nhà toán học Heron thành Alexandria.

Để chứng minh công thức Heron, ta có thể sử dụng hai cách tiếp cận chính dựa trên các hệ thức lượng giác. Mỗi cách đều có những ưu điểm riêng và phù hợp với các tình huống khác nhau trong giải toán.

Các hệ thức trong công thức Heron được xây dựng dựa trên mối quan hệ giữa diện tích tam giác và các yếu tố hình học của nó. Việc chứng minh sẽ được triển khai theo hai hướng chính: sử dụng định lý cosin và áp dụng công thức diện tích tam giác với góc.

Chứng minh công thức Heron dựa trên định lý cosin

Xuất phát từ định lý cosin trong tam giác ABC với các cạnh a, b, c, ta có:

cos A = (b² + c² – a²)/(2bc)

Thay cos A vào công thức tính diện tích tam giác S = (1/2)bc.sin A và biến đổi:

sin A = √(1 – cos²A)

Sau khi thực hiện các phép biến đổi đại số, ta thu được công thức Heron:

S = √(p(p-a)(p-b)(p-c))

Trong đó p = (a+b+c)/2 là nửa chu vi tam giác.

Chứng minh công thức Heron dựa trên diện tích và góc tam giác

Phương pháp chứng minh công thức Heron này bắt đầu từ công thức tính diện tích tam giác theo góc:

S = (1/2)bc.sin A

Kết hợp với các hệ thức lượng giác cơ bản:

sin²A + cos²A = 1

sin A = 2sin(A/2)cos(A/2)

Qua các bước biến đổi toán học và đặt p = (a+b+c)/2, ta có thể chứng minh được công thức Heron:

S = √(p(p-a)(p-b)(p-c))

Kết quả này hoàn toàn trùng khớp với công thức Heron ban đầu, khẳng định tính đúng đắn của phương pháp chứng minh.

Các dạng bài tập thường gặp về công thức Heron

Công thức Heron là một trong những công thức quan trọng trong hình học. Công thức Heron giúp tính diện tích tam giác khi biết độ dài ba cạnh, đặc biệt hữu ích trong các bài toán không thể áp dụng công thức thông thường. Dưới đây là các dạng bài tập phổ biến giúp các em rèn luyện kỹ năng sử dụng công thức này.

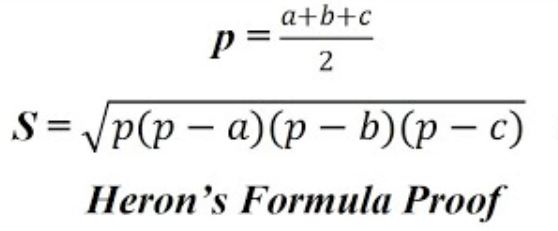
Bài tập tính diện tích tam giác khi biết ba cạnh

Để giải các bài toán tính diện tích tam giác bằng công thức Heron, trước tiên cần xác định nửa chu vi tam giác p = (a + b + c)/2. Sau đó áp dụng công thức Heron S = √(p(p-a)(p-b)(p-c)) để tìm diện tích. Việc tính toán cần thực hiện theo trình tự để tránh sai sót.

Một ví dụ điển hình là bài toán tính diện tích tam giác có ba cạnh 13cm, 14cm và 15cm bằng công thức Heron. Đây là dạng bài tập cơ bản giúp học sinh làm quen với cách áp dụng công thức và rèn luyện kỹ năng tính toán chính xác.

Bài tập tìm cạnh tam giác khi biết diện tích và hai cạnh còn lại

Trong các bài toán tìm cạnh tam giác sử dụng công thức Heron, việc biến đổi công thức thành phương trình bậc hai là bước quan trọng. Phương pháp giải yêu cầu kỹ năng biến đổi đại số và kiểm tra điều kiện của tam giác.

Quá trình giải thường bao gồm việc thay các giá trị đã biết vào công thức Heron, sau đó biến đổi thành phương trình bậc hai theo cạnh cần tìm. Kết quả cần được kiểm tra để đảm bảo thỏa mãn điều kiện tồn tại của tam giác.

Bài tập chứng minh liên quan đến công thức Heron

Các bài toán chứng minh thường yêu cầu vận dụng linh hoạt các tính chất của tam giác kết hợp với công thức Heron. Việc biến đổi các biểu thức và thiết lập mối liên hệ giữa các yếu tố trong tam giác là kỹ năng cần thiết khi áp dụng công thức Heron.

Một số bài toán đòi hỏi chứng minh các bất đẳng thức liên quan đến diện tích tam giác. Trong trường hợp này, việc áp dụng công thức Heron kết hợp với các phương pháp đại số sẽ giúp đưa ra lời giải thuyết phục.

Các bài tập chứng minh còn giúp phát triển tư duy logic và khả năng phân tích vấn đề một cách hệ thống. Điều này rất có ích trong việc nâng cao kỹ năng giải toán hình học nói chung và ứng dụng công thức Heron nói riêng.

Một số mở rộng và ứng dụng của công thức Heron

Ngoài việc tính diện tích tam giác thông thường, công thức Heron còn có nhiều ứng dụng mở rộng quan trọng trong hình học và thực tiễn. Công thức Heron đặc biệt hữu ích khi giải quyết các bài toán liên quan đến tam giác có ba cạnh mà không biết các yếu tố khác như góc hay đường cao.

Việc mở rộng công thức Heron giúp tính được diện tích của nhiều hình phức tạp hơn như tứ giác nội tiếp hay đa giác đều. Điều này mở ra nhiều khả năng ứng dụng trong các lĩnh vực thực tế như xây dựng, kiến trúc và đo đạc địa hình.

Tính diện tích tứ giác nội tiếp

Công thức Heron có thể được mở rộng để tính diện tích tứ giác nội tiếp thông qua công thức Brahmagupta. Diện tích tứ giác nội tiếp ABCD được tính bằng căn bậc hai của tích (p-a)(p-b)(p-c)(p-d), trong đó p là nửa chu vi và a, b, c, d là độ dài các cạnh.

Phương pháp mở rộng từ công thức Heron này đặc biệt hữu ích khi không thể xác định được đường chéo hoặc góc của tứ giác. Việc áp dụng công thức này giúp đơn giản hóa quá trình tính toán và mang lại kết quả chính xác.

Ứng dụng công thức Heron trong các bài toán thực tế

Trong lĩnh vực xây dựng, công thức Heron được sử dụng để tính diện tích các mảnh đất không đều. Ví dụ, các công ty xây dựng đã áp dụng công thức Heron để tính diện tích khu đất tam giác tại các dự án, chỉ cần đo 3 cạnh mà không cần đo góc hay đường cao.

Trong ngành đo đạc địa hình, công thức Heron giúp xác định diện tích các khu vực địa hình phức tạp bằng cách chia thành các tam giác nhỏ. Phương pháp này được các chuyên gia địa chính ưa chuộng vì tính đơn giản và độ chính xác cao của công thức Heron.

Ngoài ra, công thức Heron còn được ứng dụng trong thiết kế cảnh quan, quy hoạch đô thị và nhiều lĩnh vực khác đòi hỏi tính toán diện tích chính xác của các hình tam giác. Việc sử dụng công thức Heron giúp tiết kiệm thời gian và tăng độ chính xác trong tính toán.

Ưu điểm vượt trội của công thức Heron

Ưu điểm lớn nhất của công thức Heron là tính đơn giản trong việc thu thập dữ liệu. Chỉ cần đo độ dài ba cạnh tam giác là có thể tính được diện tích chính xác, không cần thiết bị đặc biệt để đo góc hay đường cao.

Công thức Heron cũng có độ chính xác cao và ít bị ảnh hưởng bởi sai số đo đạc so với các phương pháp khác. Điều này làm cho công thức Heron trở thành lựa chọn ưu tiên trong nhiều ứng dụng thực tế.

Tính phổ quát của công thức Heron cũng là một ưu điểm lớn. Công thức này áp dụng được cho mọi loại tam giác, từ tam giác vuông, cân, đều cho đến tam giác thường, giúp giải quyết đa dạng các bài toán hình học.

Kết luận

Công thức Heron là một trong những phương pháp hiệu quả nhất để tính diện tích tam giác khi biết độ dài ba cạnh. Gia Sư VietEdu đã hướng dẫn các em chi tiết từng bước áp dụng công thức Heron cùng với cách chứng minh và các bài tập thực hành. Việc nắm vững công thức Heron không chỉ giúp các em giải quyết nhanh chóng bài toán hình học mà còn mở rộng kiến thức về các ứng dụng của nó trong thực tế. Hãy thường xuyên luyện tập để thành thạo công thức Heron và áp dụng hiệu quả vào học tập cũng như cuộc sống.